So far, we have been concerned with the general and special kinds of propositions taken alone and in themselves. There is another aspect that must be considered. This aspect is the relationship which the propositions have to each other. This gives us what are called the properties of propositions when they are compared to each other.
This does not mean that we compare propositions indiscriminately one with another. "Birds have wings" and "Fish have fins." Both of these are propositions. Yet, you can obviously see that there is nothing to compare them with each other. There must be some ground for comparison. The ground is found in this: The terms used as subject and predicate are kept, but there is a change in quality, quantity, or both in the comparison. For example: 'All men are mortal' and 'No men are mortal.' 'Some men are mortal.' 'Some men are not mortal.'
Truth and falsity are linked in these propositions because they are opposed to each other. To say that 'All men are mortal' and to say that 'No men are mortal' clearly stand in opposition one to the other. If the first proposition is true, namely, 'All men are mortal,' what about the truth of the other propositions? So also, viewed the falsity of the one, what is to be said of the truth of the other?
A careful inspection of this logical opposition between such propositions will be important in concluding as to their truth and falsity and will help greatly to detect and refute errors during argumentation.
An investigation into the nature of logical propositions will show us how the three laws of thought are necessary to every proposition. All truth is based on these three laws of thought. What are they? They are : the Principle of Identity; the Principle of Contradiction and the Principle of Excluded Middle.
These principles need no proof because they are self-evident. Their simple explanation will show their truth.
The Principle of Identity states: "Whatever is, is.' It is also expressed in similar words: "Everything is what it is." Or, "A thing is identical with itself." This truth is self-evident. It is enough to state the principle to show its truth. Thus, when we say that something is, we identify it as existing, or at least able to exist.
The Principle of Contradiction is expressed as follows: Whatever is, cannot at the same time not be." Other expressions of the same principle are these: "It is impossible for the same thing both to be and not to be at the same time." This is really another way of expressing the Principle of Identity: if the first is true, then the second is also true. As self-evident as this is, you would be surprised to observe how this basic truth of thought is violated by even people trained in logic. But, of course, the individuals who violate this basic law of thought actually know they are doing this; their purpose is to confuse others with a confusion of terms, the actual meaning of which many people are not accurately familiar with.
If a thing 'is,' it cannot be said of it that it 'is not.' To do so asserts that 'is' would be identical with 'is not,' and 'being' would be the same as 'not being,' and a 'thing' would be 'nothing.' This would be absurd on the very face of it.
It is understood, of course, that we must use the principle of the same thing at the same time under the same circumstances. A person may 'sit and stand' at different times, but he cannot 'sit and stand at the same time.' That would be a contradiction, and therefore, untrue. A person may be 'a boy and a man' at different periods of life, but not at the selfsame moment of life.
The Principle of Contradiction applies with equal force to the order of reality and to the order of thought. However, we are here more concerned with its use in the logical order of thought only. For this reason logicians say: 'the same attribute cannot at one and the same time be both affirmed and denied of the same thing.'
The Principle of Excluded Middle is stated as follows: 'A thing either is or is not.' There are other ways to express this principle, such as: "Everything must either be or not be"; "any attribute must be either affirmed or denied of any given subject"; "two contradictories cannot be false together"; " one of the two contradictories must be true"; "between affirmation and denial there is no middle course"; "between two contradictories a middle is excluded." This should be obvious. There is no middle stage or state possible between 'is' and 'is not'; it either 'is' or 'is not.'
When applied to the logical order (the order of thought), the Principle of Excluded Middle has the necessary meaning: "If I make an affirmation, I thereby deny its contradictory; if I make a denial, I thereby affirm its contradictory."
Please keep in mind that here we have the fundamental laws and principles of correct thinking and truth. If anyone would arrive at truth, these fundamental laws must be observed. Becoming familiar with them and having them ever in mind, there will be no difficulty in understanding the properties of propositions when they are place in opposition to each other.
The logical opposition of propositions is the relation which exists between oppositions having the same subject and the same predicate, but differing in quality, quantity, or in both.
It always seems that we are faced with a demand for insurmountable effort when it comes to improving ourselves and sharpening our powers of understanding and discernment. Actually, as we think about it, the more complex things appear, the more simple they really are. The true philosopher sits on the pinnacle of knowledge. There are only four possible ways in which a proposition, having the same subject and the same predicate, may appear. Only four! These four ways are as follows: (A) a universal affirmative; (E) a universal negative; (I) a particular affirmative; (O) a particular negative. We saw these terms earlier in our study of logic.
Did you know that all the immense complexity of computers which seems so formidable is nothing more than combinations of '0' and '1'? That's right. All the information and calculations in the entire world have been reduced to series of zeros and ones. These humble ciphers control the storage and exchange of immense libraries. If the difference of a '0' or a '1' is so essential for correctness, can you imagine the importance of learning the simple laws and procedures in the science of logic - the science of right thinking?
The interesting part of the study of logic is that we would be learn it without effort if we would begin with a love for truth. We already have the essence of logic built in us - like the '0' and '1' of computer science.
Examples help to make things clear - most of the time. So, let's use an example: 'All men are learned.' What kind of proposition is this? You are correct: It is a universal affirmative. 'All' makes it universal; and, the verb form 'are' makes it affirmative. 'No men are learned.' You are correct again if you said this proposition is a universal negative. 'No men' takes in everyone. Here, the subject has been made the universal negative, while the verb remains in the affirmative 'are' learned. 'Some men are learned' is a particular affirmative proposition. Why? Because 'some' excludes certain men who are not learned. It is, therefore, a particular affirmative proposition. 'Some men are not learned' is, as you will conclude, a negative particular proposition. This is true because 'some' excludes the idea of 'all' men; and, the negative particle 'not' negates the content of the participle 'learned.'
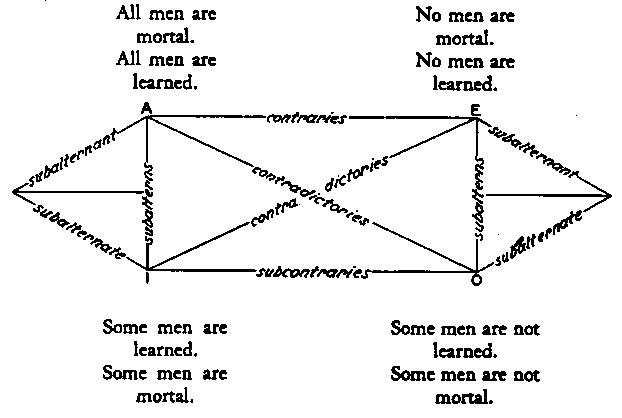
These propositions exemplify the four types of opposition. This opposition, together with their mutual relations as 'opposites,' is shown in what is called the Square of Opposition:

The diagram shows the four types of opposition and the four relations resulting from this opposition.
The relation of subalternation is the opposition existing between a universal and particular affirmative ( A and I), and between a universal and particular negative (E and O). Both propositions, the universal and the particular, are called subalterns. The universal is the subalternant (A and E), while the particular is the subalternate (I and O).
The relation of contradiction is the opposition existing between a universal affirmative (A) and a particular negative (O), and between a universal negative (E) and a particular affirmative (I).
The relation of contraraiety is the opposition existing between a universal affirmative (A) and a universal negative (E).
The relation of subcontraraiety is the opposition existing between a particular affirmative (I) and a particular negative (O).
Laws of Logical Opposition.
It does not require much concentration to perceive that these different relations of opposition make it possible for us to formulate certain laws of truth and falsity regarding propositions having these various relations. We will examine these now.
A - I and E - O. There are two parts to this law: the first part states: the truth of the universal involves the truth of the particular; but the truth of the particular does not involve the truth of the universal. This means, then, that if A is true, I must also be true; if E is true, O must be true, also. An explanation will be sufficient to prove the truth of this rule. What is true of 'all' individuals of a class must also be true of 'some' of these individuals. The reason is this: What is true of the 'whole' must also be true of every 'part.' If "All men are mortal," then, obviously, "Some men are mortal." If "All dogs are not cats," then "Some dogs are not cats" either.
If I (particular affirmative) is true, we cannot conclude that A (universal affirmative) is true; and if O (particular negative) is true), we cannot conclude that E (universal negative) is true. This is quite clear, because what is true of 'some,' need not be true of 'all'; because what is true of a 'part' of a class, need not be true of the 'whole' class. Now we should recognize that it may be true, but it need not be so. It might happen that what is said of 'some' affects the 'whole' class too, but we cannot argue validly in virtue of the proposition from 'some' to 'all,' or from the 'part' to the 'whole.'
To use the previous 'learned' example: Just because 'Some men are learned' it cannot be concluded that 'All men are learned.' Likewise, because 'Some men are not learned' this does not entitle us to argue that 'No men are learned.' We are not warranted to judge from the truth of the particular to the truth of the universal, even though at times we might hit on the truth. For example: 'Some men are mortal,' hence 'all men are mortal.' 'Some men are not irrational,' hence 'All men are not irrational.' No valid conclusion flows from the particular to the universal. In such cases, the universal will always be doubtful.
The second part of the law of subalternation states: the falsity of the particular involves the falsity of the universal; but the falsity of the universal does not involve the falsity of the particular.
What does this mean? It means that if I (particular affirmative) is false, A (universal affirmative) is false; if O (particular negative) is false; E (universal negative) is false. This is the first part of the rule. For something to be true of 'all,' it must be true of each and every individual making up the 'all.' And, that something be true of the 'whole,' it must be true of every 'part' contained in the 'whole.' We ask the question: How could something be true of the 'all,' if it is false of 'some'? Thus, if it is false that 'Some men are learned,' it is certainly false to state that 'All men are learned'; and if it is false to say that 'Some men are not mortal,' it is also false to say that 'All men are not mortal.' From the falsity of the particular, it must be concluded to the falsity of the universal.
The second part of this rule states: If A (universal affirmative) is false, I (particular affirmative) need not be false; and if E (universal negative) is false, O (particular negative) need not be false. For a universal to be true, every individual of the class and every 'part' of the 'whole' must be true. Consequently, the universal will be false, if not every individual of the universal and not every 'part' of the 'whole' is true.
What does this mean? It means that if a universal is false, some of its individuals must also be false, but some may be true - some of the others, that is. Here, too, all of the individuals may be false, but the falsity of the universal only permits us to conclude that some of the individuals are false, leaving the matter undecided whether the others are true or false.
For example: if it is false that 'All men are learned,' it cannot be said it is false that 'Some men are learned.' The only thing that can be concluded from the falsity of 'All men are learned,' is that 'Some men are not learned.'
Similarly, if it is false to say that 'No men are learned,' one does not have the right to conclude that it is false to say that 'Some men are not learned.' The only legitimate conclusion that may be drawn is that 'Some men are learned.' And so, the falsity of the universal does not involve the falsity of the particular: the particular may or may not be false together with the universal. In such cases, the falsity of the subalternate will always be in doubt when the subalternant is false.
A - O and E - I. This law also has a two-fold phase. The first rule is: contradictories cannot be true together. Thus, if A is true, O is false; if O is true, A is false; if E is true, I is false; if I is true, E is false. In an affirmative universal (A) proposition, it is asserted that the predicate is affirmed of each and every individual belonging to the subject: 'All men are mortal.' If this is true, then it must be false to deny this statement of 'some'; thus, the statement that 'Some men are not mortal (O) cannot be true. In a negative universal (E) proposition, it is asserted that the predicate must be denied of each and every individual belonging to the subject: 'No saints are sinners.' If this statement is true, then it must be false to say that 'Some saints are sinners' (I). Therefore, what is true of all, must be true of every one of the class; to state at the same time that 'all are' and 'some are not,' and that 'none are' and 'some are,' would violate the Principle of Contradiction. If, then, the universal affirmative (A) is true, the particular negative (O) is false; and if the universal negative (E) is true, the particular affirmative (I) is false.
The law works also in reverse: if O is true, A is false; and if I is true, E is false. If it is true that 'Some men are not learned,' it is certainly false to assert that 'All men are learned'; and if it is true that 'Some dogs are poodles,' it must be false to assert that 'No dogs are poodles.' From the truth of the particular negative (O), then, it follows that the universal affirmative (A) is false. Likewise, from the truth of the particular affirmative (I) follows the falsity of the universal negative (E).
The second rule of the law of contradiction states: contradictories cannot be false together. If A is false, O is true; if E is false, I is true; if O is false, A is true; if I is false, E is true. The demonstration of this rule is nothing more than a variation of the preceding rule and should pose no difficulty. If it is false that 'All men are learned,' it must be true that 'Some men are not learned' ( A -O). Now, if it false that 'No men are learned,' it must be true that 'Some men are learned' (E - I).
Also, if it is false that 'Some men are not mortal,' it must be true that 'All men are mortal.' If it is false that 'Some men are baboons,' it must be true that 'No men are baboons.'
Observe that in all these examples, when 'some' is placed in opposition to 'all,' we must remember that 'some' is equivalent to 'at least one, and possibly more.'
We see now the correctness of the following conclusions: from the falsity of the affirmative universal (A) follows the truth of the particular negative (O); and, from the falsity of the universal negative (E) follows the truth of the particular affirmative (I). Also, from the falsity of the particular negative (O) follows the truth of the universal affirmative (A); and from the falsity of the particular affirmative (I) follows the truth of the universal negative (E).
Notice that the contradictory pairs form a perfect opposition among themselves. They can be neither true nor false together; one must be true and the other must be false. It follows from this that to reject the truth of any proposition, the contradictory of that statement must first be proven. This alone is required and is sufficient. For example, if anyone makes the general assertion that 'No statements of John Paul II are heretical,' all that would be needed to break down the truth of this statement would be to prove a single instance showing that 'At least one statement of John Paul II is heretical,' because that would entitle a person to make the contradictory statement that 'Some (meaning: at least one, possibly more) statements of John Paul II are heretical.' The reason for this is that there is no neutral middle ground between contradictories as we have seen in the Principle of Contradiction. Namely: A thing either is or is not; if the one is true, the other must necessarily be false.
A - E. The rules state: contraries cannot be true together; contraries may be false together.
If A is true, E is false; if E is true, A is false. If A is false, E may be true or false; if E is false, A may be true or false.
That the first rule is correct may be seen with the help of the 'square of opposition.' Let us assume that the universal affirmative (A) is true: 'All men are mortal.' The result of this would be, according to the Law of Contradiction, that O must be false. That is, it would be false to say that 'Some men are not mortal.'
According to the Law of Subalternation: 'The falsity of the particular involves the falsity of the universal.' As a consequence, E (universal negative) is false, and the statement that 'No men are mortal' (E) cannot be true. If, then, A is true, E is false. The same line of reasoning applies, if we suppose E (the universal negative) to be true: 'No stones have life.' If E is true, its contradictory (I) must be false, namely, 'Some stones have life.' And, since this particular affirmative (I) is false, it also involves the falsity of its universal (A), according to the Law of Subalternation. Therefore, 'All stones have life' is also false. If E is true, A must be false. And so, it is shown that contraries cannot be true together.
The second rule is proven in a like manner by means of the 'square of opposition.' Example: If it is granted that A (universal affirmative) is false: 'All fishes have lungs' and since this is false, its contradictory (O) must be true: 'Some fishes have no lungs.' But, we have seen from the Law of Subalternation, that 'the truth of the particular does not involve the truth of the universal.' Thus, although it is true that 'some fishes have not lungs' (O), we cannot conclude from this that its universal (E) is also true and say that 'No fishes have lungs.' E may be false. Hence, both contraries may be false. Likewise, if it is granted that E, the universal negative is false: 'No professors are learned,' this would make the contradictory (I) true: 'Some professors are learned.' Here again, we observe that 'the truth of the particular does not involve the truth of the universal.' Conclusion: the truth of A is not established; it may be true to say 'All professors are learned,' but it may also be false. Thus, both contraries may be false.
What can we conclude from all this? We can conclude the following: From the truth of one contrary we can conclude to the falsity of the other; but from the falsity of one contrary we cannot conclude to the truth of the other. The reason is simple. The contraries are the two extremes in a certain sphere with a middle ground in between: like 'black' and 'white' in the sphere of color. The middle ground between these two colors is red and green and blue and other colors. Of course, if something is 'white' it cannot be 'black' or any other color. But if it is not' white,' it need not be 'black,' simply because it could be some other color like red, blue, green, yellow - or whatever. Similarly, if it is not 'black,' it need not be 'white.' It could be some other color. This illustration shows that the same relation exists between contrary propositions.
I - O. There is a double rule here also. It states: both subcontraries cannot be false; but both subcontraries may be true.
The first rule requires: If I is false, O is true; if O is false, I is true. Let us take for granted that the particular affirmative (I) is false: 'some men are handicapped.' Its contradictory (E) must be true: 'No men are handicapped.' But, the supposition is that the particular negative (O) is also false: 'Some men are not handicapped.' As a consequence, its contradictory (A) must be true: 'All men are handicapped.' Therefore, if both I and O could be false together, the result would be that A and E would be true together; but we have proven by the Law of Contraries that contraries cannot be true together. Therefore, suubcontraries cannot be false at the same time; at least one of the two must be true.
The second rule of the subcontraries states that both may be true together: if I is true, O may be true; if O is true, I may be true. Let us suppose that I is true: 'Some men are handicapped.' The contradictory of this (E) must be false, and we cannot say that 'No men are handicapped.' We know from the Law of Subalternation that 'the falsity of the universal does not involve the falsity of the particular.' Hence, even though E is false, we cannot conclude to the falsity of O: the proposition O may be true that 'Some men are handicapped.' The argument can also be reversed: If O is true, 'some men are not crippled,' then its contradictory A is false that 'All men are handicapped.' Since we cannot conclude from the falsity of a universal to the falsity of the particular (Law of Subalternation), we cannot infer that I is also false: the statement that 'Some men are handicapped' may be true. Both contraries, therefore, may be true together.
Although all this seems to be nothing more than mental gymnastics, perseverance in understanding these rules governing the opposition of propositions will help immensely in sifting through the seemingly endless mass of propaganda aimed at gaining one's approval and loyalty for some pre-determined plan. The whole purpose in getting people not to think, is so that they will be confused and make the wrong choices. The choices are wrong for them; but they are right for the manipulators and exploiters. All that has been said above seems to be confusing. However, if a little time is dedicated to sharpening our thinking tools that have grown dull with disuse, the results will be most gratifying.
The results of the four types of opposition (Namely, subalternation, contradiction, contrariety, subcontrariety) may be summarized in the following list of legitimate conclusions:
If A is true: then I is true, E is false, O is false.
If A is false: then O is true, E is doubtful, I is doubtful.
If E is true: then O is true, A is false, I is false.
If E is false: then I is true, A is doubtful, O is doubtful.
If I is true: then E is false, A is doubtful, O is doubtful.
If I is false: then O is true, A is false, E is true.
If O is true: then A is false, E is doubtful, I is doubtful.
If O is false: then I is true, E is false, A is true.
From the necessary relations of 'opposites' it is clear that we are frequently justified to conclude from the truth or falsity of one proposition to the truth or falsity of another. This method of concluding from the truth or falsity of one statement to the truth or falsity of another is called immediate inference. It is called 'immediate' because we can pass directly from the one to the other, without the necessity of adducing any other idea or judgment as proof. The 'square of opposition' and the Three Laws of Thought are enough to make their truth or falsity evident, provided we know beforehand that one of these opposites is true or false.
A knowledge of the 'square of opposition' and its application will prove to be a powerful help in correct thinking. The advantage lies in the fact that we do not have to spend endless and fruitless time attempting to prove everything when it is really sufficient to prove one thing, then apply the rules which have been presented here. Because knowledge is power, the study of logic has all but been abandoned. Because people who know how to think are a threat to tyrants and a danger to the devious, every effort is used to keep people from thinking correctly.
All that has been said on the subject of opposition of propositions may be summarized as follows:
Propositions are said to be logically opposed to each other, when they have the same subject and predicate, but with a change in quality or quantity or both.
All truth is based upon the three laws of thought: the Principle of Identity, the Principle of Contradiction, and the Principle of Excluded Middle.
The Principle of Identity states: 'Everything is what it is.' The Principle of Contradiction states: 'It is impossible for the same thing both to be and not to be at the same time.' The Principle of Excluded Middle states: 'Everything must either be or not be (something).'
These principles are self-evident and they underlie all being and thinking.
The 'square of opposition' illustrates the four types of logical opposition possible between propositions: subalternation, contradiction, contrariety, and subcontraraiety.
Subalternation is the opposition existing between A and I, and between E and O. The two rules for subalternation are: The truth of the universal involves the truth of the particular, but the truth of the particular does not involve the truth of the universal; the falsity of the particular involves the falsity of the universal, but the falsity of the universal does not involve the falsity of the particular.
Contradiction is the opposition existing between A and O and between E and I. The two rules are: contradictories cannot be true together; contradictories cannot be false together.
Contrariety is the opposition existing between A and E. The two rules are: contraries cannot be true together; contraries may be false together.
Subcontrariety is the opposition existing between I and O. The two rules are: both subcontraries cannot be false; both subcontraries may be true.
This method of concluding from the truth or falsity of one statement to the truth or falsity of another is called immediate inference.
'A' is the universal affirmative proposition; 'I' is the particular affirmative proposition. 'E' is the universal negative proposition; 'O' is the particular negative proposition.
If all truth is contained in the judgment, and the judgment is expressed in a proposition, it follows necessarily that a clear understanding of the laws concerning propositions is essential for correct thinking. Cracked thinking if not maliciously deliberate, is still cracked thinking and can never lead to truth.
A physician who administers a deadly remedy to a patient may do so out of malice or by accident. As far as the patient is concerned, it makes no difference to him whether the poison was given to him deliberately or accidentally: he is still dead! Does it make a great difference for those who are misled, whether this was done deliberately or not? Being 'misled' means to be guided in a wrong direction - a direction which does not lead to a proposed goal. Neither malice nor good intentions will protect the person who follows wrong guidance. A badly aimed bullet will speed in no other direction than that in which it has been directed. If this is true of the laws of nature established by the Lawgiver, what law of right reasoning permits us to reason that this same Lawgiver has no laws governing the most important aspect of our existence: salvation?
Even a cursory reading of this instruction on the opposition of propositions will already have alerted the persevering reader to the fact that false reasoning like false faith cannot lead to a happy conclusion. This is why there has been born a truism: 'Hell is paved with good intentions.'
Denial of Faith. Direct denial of faith is made by words, signs or actions which by their nature contain a denial of the true faith or a profession of a false faith. It is a direct denial of faith to participate in Protestant worship services. John Paul II's visit to England in 1982 and his public statements to the heretical minister of the Church of England, Mr. Runcie, to wit: "We are sister Churches…" is a direct denial of the true faith by words; his presence among promoters of a false religion and his praying to the "Christian martyrs of the 20th century" among whom Martin Luther King, Jr. was one is tantamount to a public admission that this man was in heaven. In the same way, John Paul II's convoking of the leaders of the various false religions to Assisi and praying together for 'peace' is a direct affirmation in sign and action of religious indifference. The Church teaches that the teacher of all false religions is Lucifer - doctor haereticorum.
Liberals, Socialists and Communists are heretics or not, depending upon the extent to which they profess the principles of their parties. Whoever, for example, professes the complete independence of the Christian State from the Church, or that the Church is subject to the State, is a heretic. Naturalism is a heresy. Therefore, those who belong to organizations promoting naturalism are heretics.
No one can be both, orthodox and non-orthodox at the same time. The Principle of Contradiction should be applied to John Paul II as well as to anyone else. Jesus Christ illustrated the Principle of Contradiction very well when He said: "You are either with me, or you are against me."
Return to Menu.